Kyo_s_s Homepage

AHC030 参加記

競技プログラミング

AHC

99位、パフォーマンスは2018でした。レート 1981 -> 2003(+22) でした。黄色になりました！

問題: https://atcoder.jp/contests/ahc030

GitHub: https://github.com/Kyo-s-s/AHC030

どんなことをしたのか書きます。

Warning

誤った解釈/主張をしている箇所があるかもしれません。その場合はX(Twitter)などで教えていただければありがたいです。 XのID: @Kyo_s_s

ベイズ推定

$P_i((x, y))$ を油田 $i$ が(左上から) $(x, y)$ だけずらした位置にある確率とします。これをもとにベイズ推定を行いました。

この定め方により、任意の $i$ に対して $\sum_{x, y} P_i((x, y)) = 1$ が成り立ちます。また、初期値は入力生成方法より一様です。

クエリ結果を $q$ とします。このとき、ベイズの定理より、

$\displaystyle P_i((x, y) \mid q) = \frac{P_i(q \mid (x, y)) P_i((x, y))}{P_i(q)}$

が成り立ちます。　また、 $P_i((x, y))$ を事前確率、 $P_i((x, y) \mid q)$ を事後確率、 $P_i(q \mid (x, y))$ を尤度と言います(あってるよね？)。

Note

$P(B \mid A)$ は、「事象 $A$ の元で事象 $B$ が起こる確率」です。

事後確率 $P_i((x, y) \mid q)$ は「クエリの結果として $q$ が返ってきた下で、油田 $i$ が位置 $(x, y)$ に存在する確率」、尤度 $P_i(q \mid (x, y))$ は「油田 $i$ が位置 $(x, y)$ にある下で、クエリの結果として $q$ が返ってくる確率」となります。

ベイズ推定では、クエリ毎に事後確率を求め、事前確率を更新していきます。つまり、クエリ $q$ を聞いたのち、

$\displaystyle P_i((x, y)) \gets \frac{P_i(q \mid (x, y)) P_i((x, y))}{P_i(q)}$

と更新します。

ここで、更新後も任意の $i$ に対して $\sum_{x, y} P_i((x, y)) = 1$ が成り立つことに注意すると、 $P_i(q)$ は陽に求める必要はなく、一旦

$\displaystyle P_i'((x, y)) \gets P_i(q \mid (x, y)) P_i((x, y))$

と更新したのち、

$\displaystyle P_i(x, y) \gets \frac{P_i((x, y))}{\sum_{x', y'} P_i'((x', y'))}$

とすればよいです。

以降、掘る/占いクエリ $q$ に対して $P_i(q \mid (x, y))$ を求めることを考えます。

掘るクエリに対する更新

座標 $(h, w)$ を掘って、油田の量が $v$ であることが分かったとします。この時のクエリを $q = (h, w, v)$ と表すこととすると、求めたい値は $P_i(q = (h, w, v) \mid (x, y))$ 、つまり「油田 $i$ が位置 $(x, y)$ にある下で、 $(h, w)$ の石油埋蔵量が $v$ である確率」です。

これは、油田 $i$ が位置 $(x, y)$ にあり、

$(h, w)$ に重ならないとき: 油田 $i$ 以外を配置して、 $(h, w)$ の石油埋蔵量が $v$ になる確率
$(h, w)$ に重なるとき: 油田 $i$ 以外を配置して、 $(h, w)$ の石油埋蔵量が $v - 1$ になる確率 ( $v = 0$ のときは $0$ )

と等しいです。これらの値は油田 $i$ 以外についてのDPをすることで求めることができます。

Warning

そのままこの値を計算すると値が小さくなりすぎてしまい、アンダーフローが起きてしまう可能性があるかもしれません。コンテスト中には気づかずそのまま実装してしまいました。

占いクエリに対する更新

座標の集合 $S = \{(h_1, w_1), (h_2, w_2), \ldots, (h_n, w_n)\}$ を占って、返ってきた値が $v$ であったとします。この時のクエリを $q = (S, v)$ と表すこととすると、求めたい値は $P_i(q = (S, v) \mid (x, y))$ 、つまり「油田 $i$ が位置 $(x, y)$ にある下で、集合 $S$ を占って $v$ が返ってくる確率」です。

先に言ってしまうと、この値は厳密に求めずに適当にしてしまいました。 なので以降の文章は適当です。

$\mathrm{normpdf}(x, \mu, \sigma)$ を、平均 $\mu$ および標準偏差 $\sigma$ の確率密度関数に $x$ を代入した値とします。

各 $v(S) = 0, 1, \ldots$ に対して、集合 $S$ を占ってクエリ結果 $v$ が返ってくる確率というのが、

$\displaystyle \int_{v-0.5}^{v+0.5} \mathrm{normpdf}(x, (|S|-v(S))\epsilon + v(S)(1-\epsilon), |S|\epsilon(1-\epsilon)) dx$

で求められます。これを $p_0, p_1, \ldots$ とします。 (ここで、 $v(S)$ は集合 $S$ の石油埋蔵量の総和です。読みづらくてすみません…) ( $x = 0$ のとき、元が負数で $0$ にまとめられるケースもあるのでこの時は $-\infty$ から $0.5$ までの積分値となります) (ぼくは問題文が読めず、積分区間を $v$ から $v + 1$ にしていました。バカ…)

Note

今回は数値積分を用いてこの値を求めたのですが、誤差関数を使うと良いらしいです(そのほうが高速？)。 Rustでは libm::erf が使えるらしいです。

油田 $i$ を位置 $(x, y)$ に置いたとき、少なくとも $v(S)$ の値は、集合 $S$ の座標の中で、油田 $i$ を位置 $(x, y)$ に置いた時に重なる個数以上になります。

重なる個数を $w$ と置き、 $P_i(q = (S, v) \mid (x, y))$ を $(\sum_{k=w}^\infty p_k) / (\sum_{k = 0}^\infty p_k)$ であるとして更新を行いました(ここが適当ポイントです、本来は他の油田の情報も考える必要があると思います)。

戦略

まず、 $N \times N$ の島を $4 \times 4$ くらいずつに分割し、占いクエリを投げます。これにより、油田がある可能性がある/ほとんどないといったことがある程度分かります。

その後、油田量の期待値が $0.6$ に近い座標を掘り、確率を更新する… ということを繰り返しました。

この手法だと終盤に確率が非常に小さい箇所をたくさん掘ってしまいます。そのため、期待値がある程度以下の座標については、掘らずにまとめて占いを行うようにしました。seed19の終盤でこの挙動をしています。

各油田について存在する位置がある程度以上特定できたとき、提出クエリを出すようにしました。

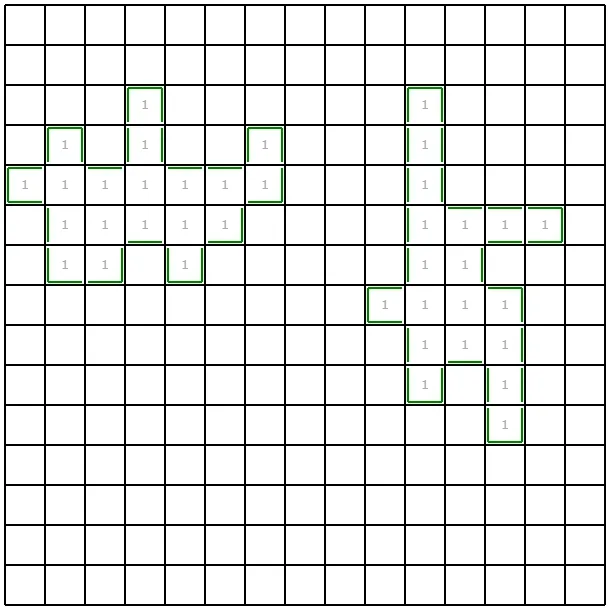seed0 seed = 0, Score = 2800000

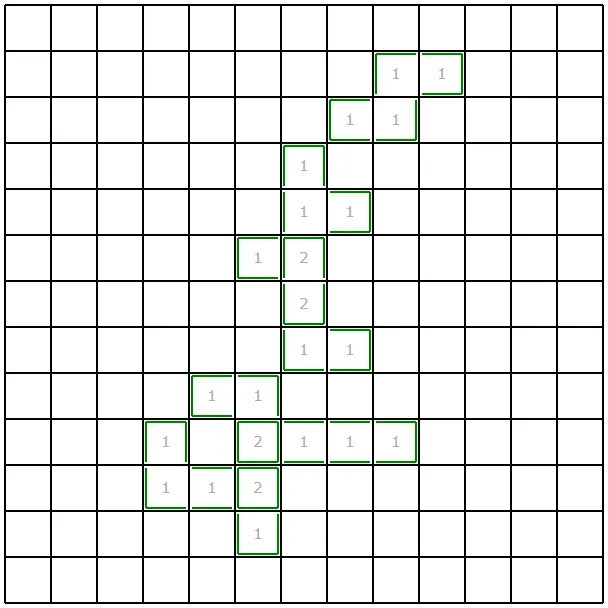seed1 seed = 1, Score = 37982051

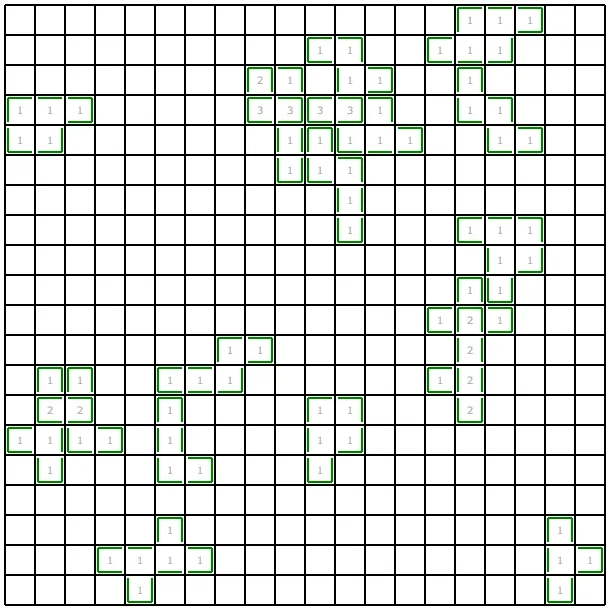seed19 seed = 19, Score = 216280847

色はその座標の油田量の期待値です。 $1$ 以上は緑、 $0$ は白として表示するようにしました。

占いで適当なことをしているため、基本は $1$ マス掘り戦略をしました。

$M$ (油田の個数) が小さいときには各配置に対してベイズ推定をする方針が強く惨敗していたのですが、 $M$ が大きいときにはそこそこ強かったらしいです ( $M=18, 19, 20$ ではそれぞれ 17, 31, 35位でした。 https://siman-man.github.io/ahc_statistics/030/index_m.html 参照)。

入力ケース生成方法によると $M$ が小さいケースが圧倒的に多く、負けてしまったようです。

この方針の課題

占いの更新の仕方が適当すぎる

困っています。ちゃんとやる方針を考えたのですが、重そうな気がしています。

同じ形の油田が存在するとまずい

困ります。同じ油田の形だと全く同じ遷移をしてしまい、確率が $1$ に収束しないためです。

今回は同じ形があったときには確率が高いものから採用するようにしましたが、終盤でこのことに気づいたため、だいぶ実装がごちゃごちゃになってしまいました。

感想

コンテスト中はこれでいいじゃん！と思っていたのですが、いざ参加記を書くと本当にこれ正しいの？と疑問に思う点や、適当すぎない？という点がたくさん出てきてしまいました。むむむ…。

とはいえこれでHeuristic黄色になりました。うれしい！この記事とは別に、Heuristic入黄記事を書くかもしれません。

もっと強くなりたい～